Bubble Sort is the most popular sorting algorithm that most programmers start with. Even though its performance is not good enough for most practical cases, it is much simpler than other efficient sorting algorithms like quick sort or merge sort.
Bubble Sort Algorithm
Bubble sort is to continuously swap two adjacent elements if they are not in right order until no swapping is required.
In programming, generally two nested loops are used. The inner loop starts from the first element and checks whether that is in right order with respect to the next element. If not, then it swaps them. Then the control moves to the next position and repeats the same thing until the control reaches to the last element.
At the end of every outer loop iteration, one element is placed at the right position. For example, if we sort the array in ascending order, then the biggest element will come to the last position after completion of the first outer loop iteration.
Similarly, after completion of the second outer loop iteration, the second biggest element takes the second last position.
In this way after n-1 iterations, n-1 elements take their right positions. And the remaining last element has to be in the right position also.
Graphical Illustration of Bubble Sort
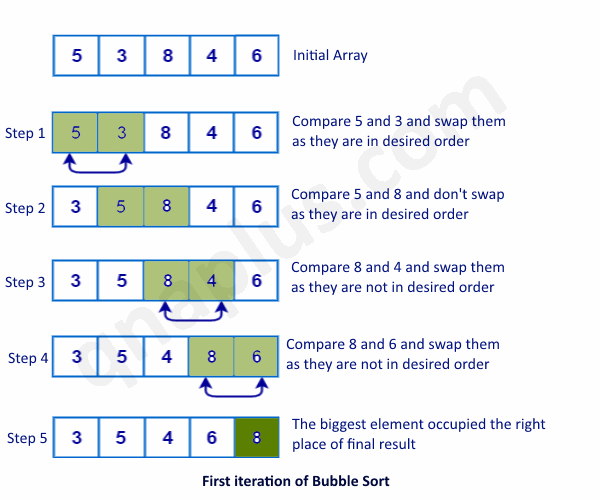
The above diagram shows the first outer loop iteration. We can see that after completion of the first iteration of the outer loop, the biggest element (here 8) comes to the last position. Similarly, after completion of second iteration, the second biggest element would come to the second last position. If we continue this process for n-1 times, then all n elements will take their right positions and the array will become sorted.
Implementation of Bubble Sort in C
We’ll implement bubble sort in C programming language here. We can implement this in various ways – in different levels of complexity and efficiency.
Variation 1:
Let’s start with the simplest one.
#include <stdio.h>
void bubble_sort(int *arr, int n)
{
int i = 0, j = 0;
int tmp = 0;
for(i = 0; i < n-1; i++)
{
for (j = 0; j < n-1; j++)
{
if(arr[j+1] < arr[j])
{
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
}
#define MAX_SIZE 64
int main() {
int arr[MAX_SIZE];
int n, i;
printf("Enter the size of the array: ");
scanf("%d", &n);
printf("Enter the array elements:\n");
for(i = 0; i < n; i++) {
printf("arr[%d]: ", i);
scanf("%d", arr + i);
}
printf("The entered array:\n");
for(i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
bubble_sort(arr, n);
printf("The sorted array:\n");
for(i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
The main() function first takes an array as input and calls the bubble_sort() function to sort that array.
Output
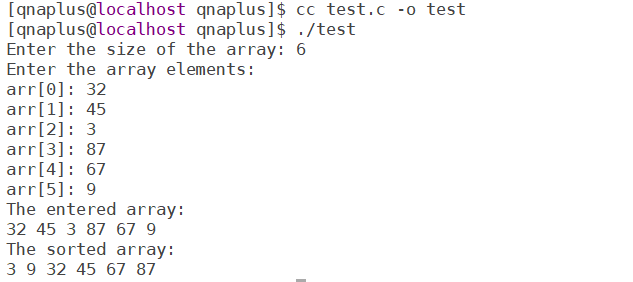
This version of the bubble_sort() function is very easy to understand. Here both the outer loop and inner loop iterate n-1 times. The inner loop starts from the first element and checks with the next element whether they are in right order. If not, then swaps them.
For example, if the current element (indexed by j) is greater than the next element (indexed by j+1), then we swap them. Then control moves to the next element.
In this case, we’ll always have (n-1)*(n-1) comparisons which is more than the maximum comparisons required by bubble sort even in the worst case scenario.
Variation 2:
Let’s see how we can improve the algorithm little bit and minimize the number of comparisons.
After completion of every iteration of the outer loop, one element is placed in the right location. That means the inner loop does not need to iterate (n-1) times all the time. It can iterate one less time after every outer loop iteration.
void bubble_sort(int *arr, int n)
{
int i = 0, j = 0;
int tmp = 0;
for(i = 0; i < n-1; i++)
{
for (j = 0; j < n-i-1; j++)
{
if(arr[j+1] < arr[j])
{
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
}We changed the loop from:
for (j = 0; j < n-1; j++)to
for (j = 0; j < n-i-1; j++)As the value of i increases, the inner loop iterates less. That way we can reduce the total number of comparisons.
Variation 3:
We can further improve the logic by terminating the outer loop if no swapping is performed by the inner loop.
No swapping in inner loop means the array already became sorted. No need to continue the outer loop after that.
void bubble_sort(int *arr, int n)
{
int i = 0;
int tmp = 0;
int swapped = 0;
do
{
swapped = 0;
for (i = 0; i < n-1; i++)
{
if(arr[i+1] < arr[i])
{
tmp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = tmp;
swapped = 1;
}
}
n = n - 1;
} while (swapped == 1);
}Here we changed the outer loop from ‘for‘ to ‘do-while’ . We could continue with the for loop also, but in this situation, a do-while loop is more appropriate.
We are reducing n by 1 (n = n-1) at the end of the inner loop such that it iterates one less time in next iteration.
The inner loop sets flag (swapped) if it performs a swapping. And outer loop continues only if ‘swapped’ flag is set.
Variation 4:
We can improve further!
In previous implementations, we were reducing the inner loop iteration by one for every outer loop iteration. But we can remember where (at which index) the last swapping happened in the inner loop. The rest of the array after that is already sorted.
In the next outer loop iteration, we can stop the inner loop where it did the last swapping in previous iteration.
void bubble_sort(int *arr, int n)
{
int i = 0;
int tmp = 0;
int newn = 0;
int swapped = 0;
do
{
swapped = 0;
for (i = 0; i < n-1; i++)
{
if(arr[i+1] < arr[i])
{
tmp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = tmp;
swapped = 1;
newn = i + 1;
}
}
n = newn;
} while (swapped == 1);
}Here the newn variable remembers where the inner loop did last swapping. Next time, the inner loop will go up to that point (up to the newn).
This is the most optimized implementation of bubble sort.
Performance of Bubble Sort
In this section, we’ll see how bubble sort performs in various conditions.
Worst Case:
The worst case is when the array is in the opposite order before we start sorting. For example, if we want to sort an array in ascending order, the array is in descending order at the beginning.
In the worst case scenario, the running time of bubble sort in Big-O notation is O(N2).
The diagram show how our four variations perform in the worst case.
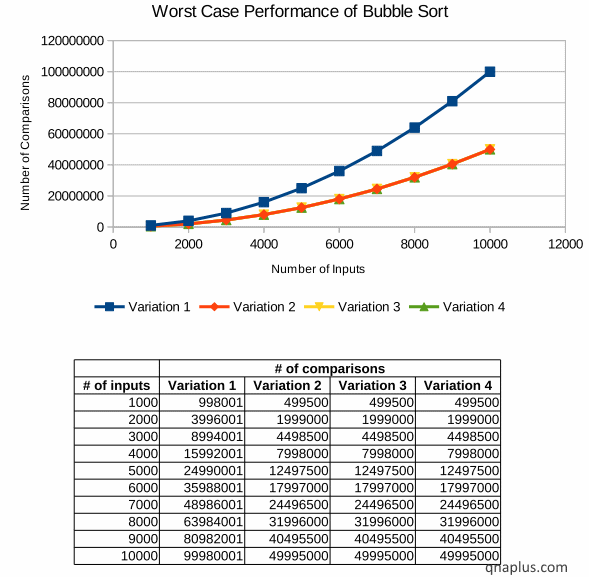
Here we can see how the number of comparison increases with the increase of the number of input elements. And the number of comparisons is directly proportional to the running time.
From the graph we can see that the first variation takes maximum number of comparisons. Other three variations take equal number of comparisons but less than that of the first variation.
We should also notice one important thing that the growth rate of all four variations is the same. If we double the number of inputs then the number of comparison becomes four times. If we increase the number of elements by four times then the number of comparisons increases by sixteen times.
It means the growth rate is O(N2).
Average Case:
The average case is when the array is in random order at the beginning.
In the average case also, the running time is O(N2).
The diagram below shows the four variations performance in this scenario.
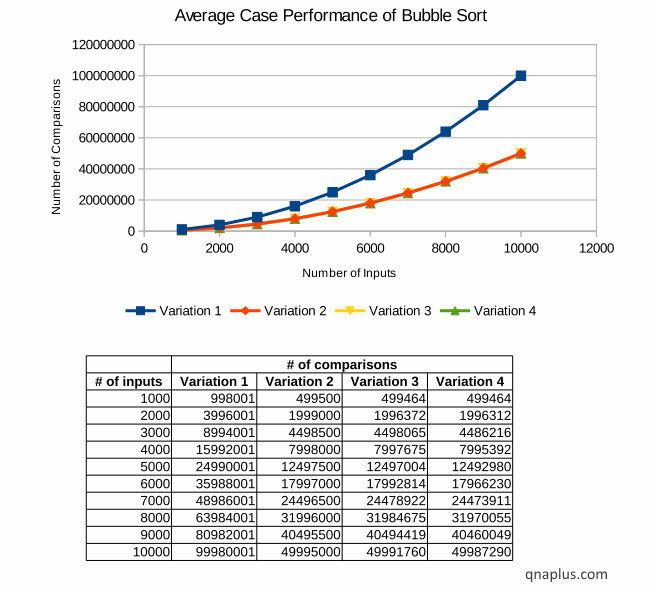
We can see that the first variation takes maximum number of comparison, then the second one, then the third one. The fourth variation takes least number of comparisons. But here also the comparison growth rate is the same, i.e. O(N2). If we double the number of inputs, the number of comparison will become four times.
Best Case:
The best case scenario is when the array is already sorted.
In this scenario, the bubble sort running time is O(N).
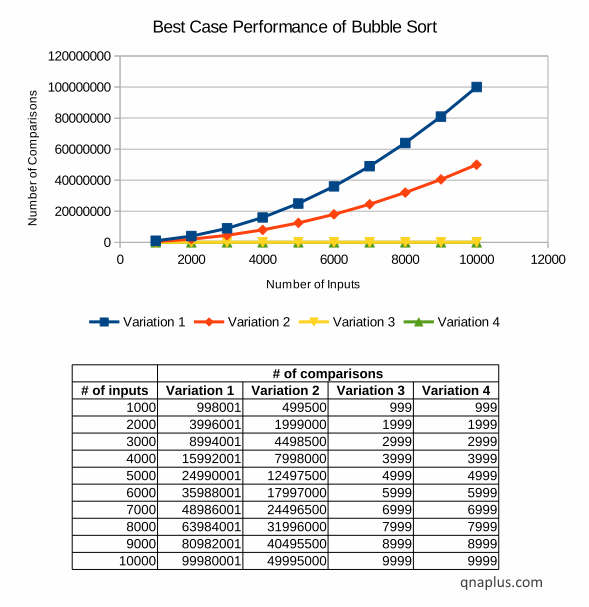
Here the comparison growth rate of first two variations is still O(N2). Second variation is slightly better than the first one in terms of actual number of comparisons. But our last two variations perform much better than the first two. The growth rate of third and fourth variations is linear. They always take n-1 comparisons.
We can see that choice of implement is important in terms of performance. The forth variation performs the best in all conditions – at least not worse than any other.