How to Implement Insertion Sort in C Programming?

Insertion sort is very popular sorting algorithms because of its simplicity. Its performance is not as good as quicksort or shellsort for large array but it is very simple like bubble sort. It is often used for less number of elements especially when the array is substantially sorted.  Here we’ll see how to implement insertion sort in C programming language. We’ll also see its performance in various conditions.

Insertion Sort Algorithm

In insertion sort, at any point of time, there will be two sub-arrays, one is sorted and the other is not. One element is taken from the unsorted sub-array and inserted in the sorted sub-array in the appropriate position such that the sorted sub-array remains sorted. This process continues until the whole array becomes sorted. At every stage we take an element and insert that in appropriate place. That’s why it is called insertion sort.

Insertion sort is often compared with the way we sort cards in our hand. We keep our cards sorted in our hand in time of dealing. When we get a new card from the dealer, our job is to insert the card at the right place such the cards in our hand remain sorted. To do that we compare the new card with the right most card in our hand. If the new card is greater than the right most card, then we place the card next to right most card, otherwise, we compare the card with the second right most card. And if the new card is greater than the second right most card then place it next to the second right most card, otherwise, continue the process until the new card gets a right place. If the new card is smaller than any card in hand, then it will get the left most position. Same thing we do with our array in insertion sort.

Graphical Illustration of Insertion Sort

This diagram shows how insertion sort works. At step 1, the array is sub-divided into two parts. First element is the first part and rest of the elements are in the second part. First sub-array will be always sorted. At step 1, as there is only one element in the left sub-array, it is sorted by default. Then we take the first element of the right sub-array and find a right place in the left sub-array to insert the element such that the left sub-array remains sorted. In this case 4 will come before 6. Similar process continues until all elements from right sub-array come into the left sorted sub-array.

Implementation of Insertion Sort in C

Here is the implementation of insertion sort in C programming.

#include <stdio.h>

void insertion_sort(int *arr, int n)
{
  int i = 0, j = 0, tmp = 0;

  for (i = 1; i < n; i++)
  {
      tmp = arr[i];
      j = i - 1;
      while(j >= 0 && tmp < arr[j])
      {
        arr[j+1] = arr[j];
        j--;
      }
      arr[j+1] = tmp;
  }
}

void main()
{
  int arr[] = {54, 66, 31, 10, 4, 77, 32, 1, 56};
  int i = 0;

  printf("Array before sorting: ");
  for (i = 0; i < (sizeof(arr)/sizeof(int)); i++) printf(" %d", arr[i]);
  printf("\n");

  insertion_sort(arr, sizeof(arr)/sizeof(int));
  printf("Array after sorting: ");
  for (i = 0; i < (sizeof(arr)/sizeof(int)); i++) printf(" %d", arr[i]);
  printf("\n");
}

The insertion_sorted() function takes an array as input and applies insertion sort algorithm on that. The outer loop iterates n-1 times where n is the number of elements. The inner loop finds the appropriate position for i-th element in first i elements in the array which are already sorted. As soon as it find the right place (j+1), it terminates. The i-th element is placed in the right place (j+1 th position) outside the inner loop.

Output of the program:

Array before sorting:  54 66 31 10 4 77 32 1 56
Array after sorting:  1 4 10 31 32 54 56 66 77

Performance of Insertion Sort

Worst case:

Running time of insertion sort in Big-O notation is O(N²) where the array is in reverse order at the beginning. For example, if we want to sort an array in ascending order and the array is in the descending order to begin with. In this case we’ll have maximum number of comparisons.

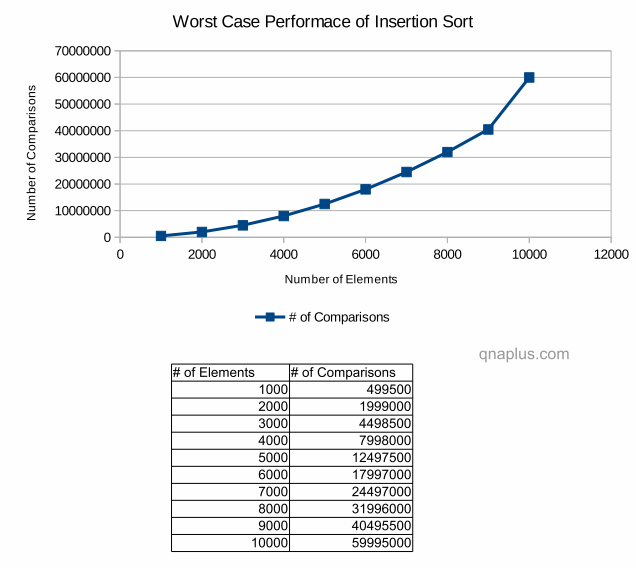
The above diagram shows how insertion sort performs in worst case condition. It shows how number of comparisons increases with the number of input elements. In this case running time is directly proportional to number of comparisons. If you look into the graph or table carefully, you’ll notice that if the number of inputs doubles, the number of comparisons increase by four times. If the number of inputs increases by four times, then number of comparisons increases by sixteen times. That’s why the running time is O(N²).

Average case:

Running time of insertion sort in Big-O notation is O(N²) where the elements are in random order to begin with.

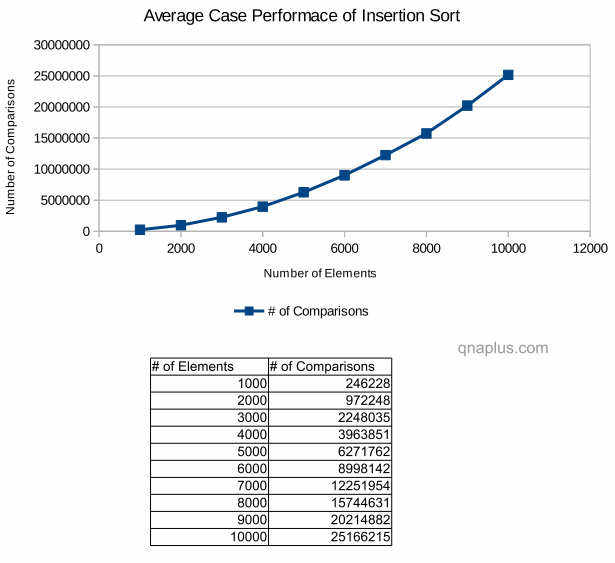
The  above diagram shows the performance of insertion sort in average case. Here the actual number of comparisons is less compare to that of the worst case. But the growth rate is same as the worst case. Here also If you double the number of input, the number of comparisons increases by four times. Similarly if the number of elements increases by four times, the number of comparisons increases sixteen times.

Best case:

Running time of insertion sort in Big-O notation is O(N) where the array is already sorted. In that case the inner loop will terminate immediately after first comparison.

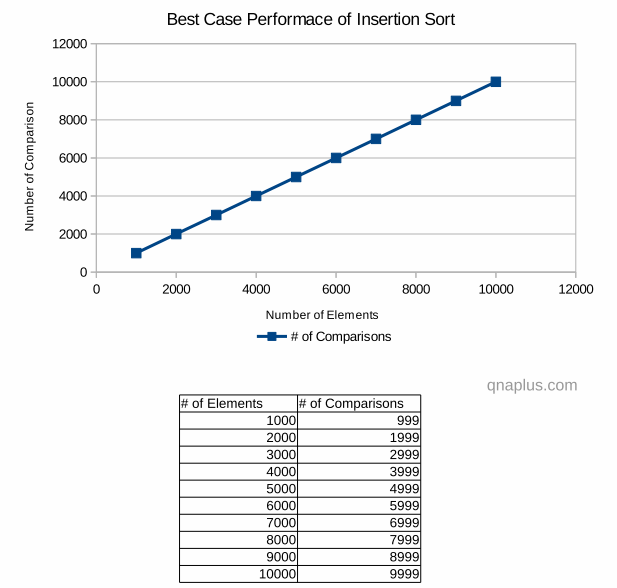
In best case the number of comparison is linear with respect to the number of inputs. That means if we double the number of inputs, the number of comparisons will also be double.

All Conditions

The diagram below compares three conditions (worst, average and best cases)

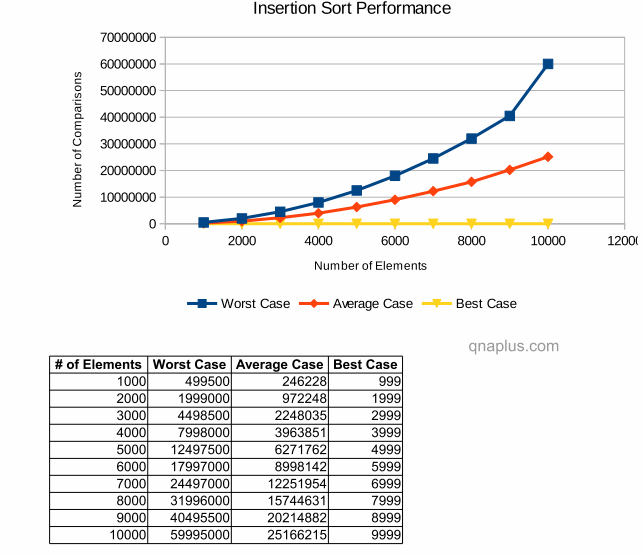
Running time in best case is negligible compare to worst or best cases for large number of input elements. Even though the time requirement for average case is always less than the worst case but their growth rate is same.

If you also want to contribute, click here.