How to Implement Merge Sort in C?

Merge sort is an efficient, general-purpose sorting algorithm. Unlike bubble sort or insertion sort, it is usable in most practical cases. Merge sort implementation is based on divide and conquer algorithm. Here we’ll see how to implement merge sort in C programming language. And also we’ll analyze its performance in various conditions.

Merge Sort Algorithm

The divide and conquer algorithm of merge sort has two parts.

1. Repeatedly divide the input array into sub-arrays until each sub-array is left with one element.
2. Repeatedly merge the sub-arrays such that the merged the sub-array becomes sorted until there is one sub-array.

Step 1 is the divide part of the algorithm. At every stage, each sub-array is divided into two parts. At the beginning, the whole array is the first sub-array. If a sub-array contains even number of elements then the divided sub-arrays will also have equal number of elements. Otherwise, one divided sub-array will have one more element than the other divided sub-array. We’ll continue this process until all sub-arrays contain only one element.

Step 2 is the conquer part, we’ll keep merging the sorted sub-arrays, such that the merged sub-arrays also becomes sorted. We’ll continue this process until we get only one sub-array which will contain all the elements of the starting array.

Graphical Illustration

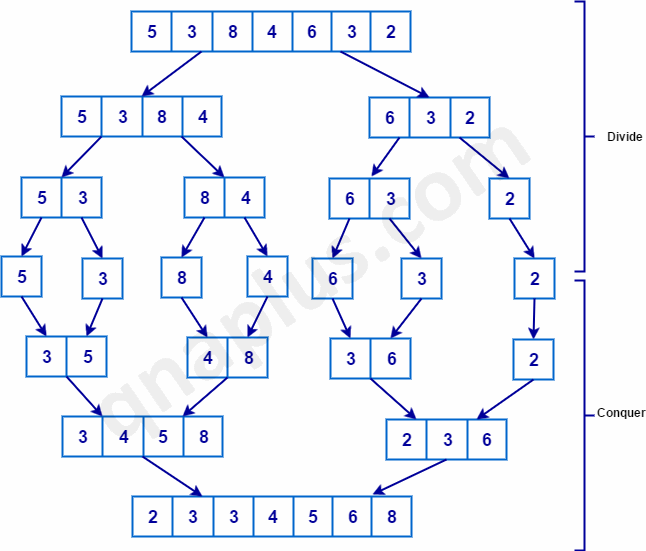
The above diagram shows how merge sort works. The array has seven elements to begin with. First the array is divided into two sub-arrays, one with 4 elements and other with 3 elements. Then they further divided into four sub-arrays. And finally in the next stage, all sub-arrays have only one element. So, all sub-arrays are sorted (array with one element is always sorted). Divide part ends here and the conquer part begins. Single element sub-arrays are merged to become two element sorted sub-arrays. Similar process continues until all elements are merged into one sorted sub-array.

Top-down Implementation of Merge Sort in C

In top-down approach, the array is divided recursively into sub-arrays until the size of each sub-array becomes 1. Then the sorted sub-arrays are merged continuously such that the merged sub-arrays become sorted. This process continues until all sub-arrays are merged into one array. Top down implementation of merge sort is more popular, widely used and easy to under stand method.

#include <stdio.h>

void merge(int *arr, int start, int mid, int end)
{
  int * tmp_arr = NULL;
  int i = 0;
  int l1 = start;
  int r1 = mid;
  int l2 = mid + 1;
  int r2 = end;

  tmp_arr = (int *)malloc(sizeof(int) * (end - start + 1));

  while((l1 <= r1) && (l2 <= r2))
  {
    if(arr[l1] < arr[l2])
      tmp_arr[i++] = arr[l1++];
    else
      tmp_arr[i++] = arr[l2++];
  }

  while(l1 <= r1) tmp_arr[i++] = arr[l1++];
  while(l2 <= r2) tmp_arr[i++] = arr[l2++];

  for(i = start; i <= end; i++) arr[i] = tmp_arr[i - start];

  free(tmp_arr);
}

void mergesort(int *arr, int start, int end)
{
  int mid = 0;

  if(start < end)
  {
    mid = (start + end) / 2;
    mergesort(arr, start, mid);
    mergesort(arr, mid+1, end);

    merge(arr, start, mid, end);
  }
}

void main()
{
  int arr[] = {54, 66, 31, 10, 4, 77, 32, 1, 56};
  int i = 0;

  printf("Array before sorting: ");
  for (i = 0; i < (sizeof(arr)/sizeof(int)); i++) printf(" %d", arr[i]);
  printf("\n");

  mergesort(arr, 0, sizeof(arr)/sizeof(int) - 1);
  printf("Array after sorting: ");
  for (i = 0; i < (sizeof(arr)/sizeof(int)); i++) printf(" %d", arr[i]);
  printf("\n");
}

Bottom-up Implementation of Merge Sort in C

In bottom-up approach, the arrays of size n is considered as n sub-arrays of size one. Then the sub-arrays are merged to together such that the merged sub-arrays become sorted. This process continues until the size of the merge sub-array becomes equal to the original array size n. Here is the bottom-up implementation of merge sort in C.

void merge(int *arr, int start, int mid, int end)
{
  int tmp_arr[100];
  int i = 0;
  int l1 = start;
  int r1 = mid;
  int l2 = mid + 1;
  int r2 = end;

  while((l1 <= r1) && (l2 <= r2))
  {
    if(arr[l1] < arr[l2])
      tmp_arr[i++] = arr[l1++];
    else
      tmp_arr[i++] = arr[l2++];
  }

  while(l1 <= r1) tmp_arr[i++] = arr[l1++];
  while(l2 <= r2) tmp_arr[i++] = arr[l2++];

  for(i = start; i <= end; i++) arr[i] = tmp_arr[i - start];
}

int min(int a, int b)
{
  return (a < b)?a:b;
}

void mergesort(int *arr, int len)
{
  int width = 0, i = 0;

  for (width = 1; width < len; width = width * 2)
  {
    for(i = 0; i < len; i = i + 2*width)
    {
      merge(arr, i, min(i + width, len), min(i + 2*width, len));
    }
  }
}

Performance of Merge Sort

Running time of merge sort in Big-O notation is O(n log n) for best, average and worst case scenarios. If we consider that merge sort take T(n) time to sort n elements, then the equation T(n) = 2T(n/2) + n follows the definition of the algorithm, where T(n/2) to sort the sub-array and n to merge two sorted sub-arrays. Applying master theorem, the running time in Big-O notation becomes O(n log n).

Diagram below show an experimental result to demonstrate the performance of the merge sort for different types of input arrays. It shows how number of comparisons increases with the increase of number of inputs.

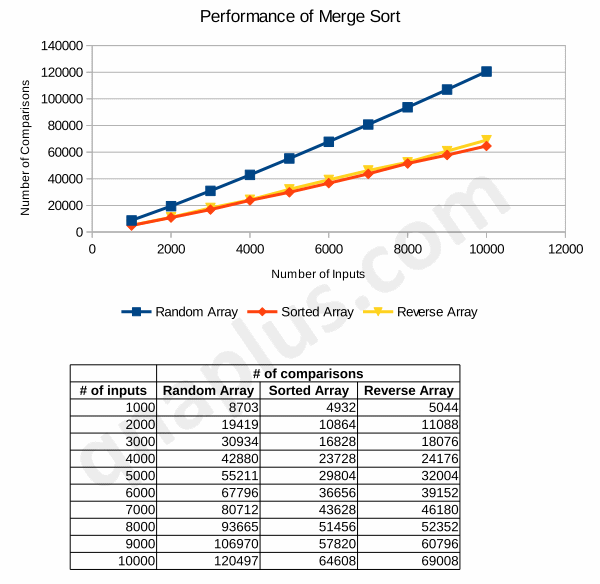
In this experiment we used three types of array. In the first array, the numbers are randomly distributed. Numbers are already sorted in the second array. And numbers are reversely sorted in the third array. Number of inputs increases by 1000 in every iteration staring from 1000. The growth rate of comparisons required is O(n log n) in all cases but actual number of comparisons differs. In case of the random array, the number of comparisons is close to n * log n, where n is the number of inputs. But in case of the sorted arrays (same order or reverse order), the actual number of comparisons is close to (n * log n ) / 2. If the array is sorted, merge sort takes half number of comparisons compared to a random array.

If you also want to contribute, click here.