How to Implement Quick Sort in C?

Quick Sort is an efficient sorting algorithm developed by Tony Hoare in 1959. It is still a commonly used sorting algorithm in most practical cases. If implemented properly, it is two or three times faster than other efficient sorting algorithms like merge sort or heap sort. Here we’ll see how to implement this sorting algorithm in C programming language. And also we’ll discuss about the algorithm and analyze the performance in various conditions.

Quick Sort Algorithm

Quick sort is a divide and conquer algorithm which is generally implemented using recursive function.

1. Select an element from the array as pivot.
2. Partition the array. One partition will have all the elements that are smaller than the pivot. Another partition will have other elements that are greater than the pivot.
3. Apply this procedure recursively with these two partitions.

Recursion will stop when a partition will have 1 or 0 element. This is the base case of the recursion. Performance of quick sort is heavily dependent on the selection of the pivot. We take different strategies based on various conditions to select the pivot to get better performance.

1. First element of the partitions is selected as pivot.
2. Last Element of the partitions is selected as pivot.
3. Random element of the partitions is selected as pivot.
4. Median of first, middle and last element of the partition is selected as pivot.

Graphical Illustration of Quick Sort

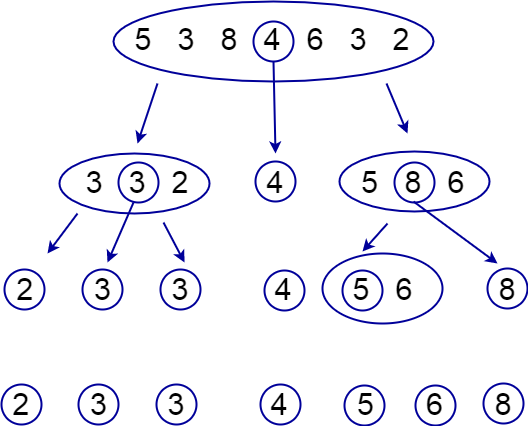
The diagram above shows how quick sort works. Middle element is selected as pivot. In this case 4 is selected as pivot in the first iteration. The array is than sub-divided into two partitions. Left partition contains all the element which are smaller than the pivot 4 and the right partition contains all the elements which are greater than 4. If we continue this procedure after 2 more iterations, the array will become sorted.

Implementation of Quick Sort in C

Here is the complete C program that implements the quick sort.

#include <stdio.h>

int partition(int *arr, int start, int end){

  int pivot, tmp, i, j;

  if(start >= end) return -1;

  pivot = start;
  i = start;
  j = end;

  while(i < j)
  {
    while(arr[i] <= arr[pivot] && i < end) i++;
    while(arr[j] > arr[pivot]) j--;

    if( i < j)
    {
      tmp = arr[i];
      arr[i] = arr[j];
      arr[j] = tmp;
    }
  }

  tmp = arr[pivot];
  arr[pivot] = arr[j];
  arr[j] = tmp;

  return j;
}

void quicksort(int *arr, int start, int end){

  int p = 0;

  if(start < end)
  {
    p = partition(arr, start, end);
    quicksort(arr, start, p-1);
    quicksort(arr, p+1, end);
  }
}

void main()
{
  int arr[] = {54, 66, 31, 10, 4, 77, 32, 1, 56};
  int i = 0;

  printf("Array before sorting: ");
  for (i = 0; i < (sizeof(arr)/sizeof(int)); i++) printf(" %d", arr[i]);
  printf("\n");

  quicksort(arr, 0, sizeof(arr)/sizeof(int) - 1);
  printf("Array after sorting: ");
  for (i = 0; i < (sizeof(arr)/sizeof(int)); i++) printf(" %d", arr[i]);
  printf("\n");
}

Performance of Quick Sort

Worst Case

Running time of quick sort in worst case scenario in Big-O notation is O(N²). Worst case scenario occurs when the pivot divides the array into two partitions of size 0 and n-1, most unbalanced partitions. In every iteration one partition would not have any element and other partition will have remaining n-1 elements. This situation occurs when smallest or biggest element is selected as pivot. One example of such situation is when we apply quick sort on a sorted array and first or last element is selected as pivot.

Best Case

Running time of quick sort in best case scenario in Big-O is O(n log n). Best case scenario occurs when pivot divides the array into two partitions of equal number of elements in every iteration. One example of such situation is when we apply quick sort on a sorted array and the middle element is selected as pivot.

Average Case

Running time of quick sort in average case scenario in Big-O notation is O(n log n). In average case, the partitions may not be equal but average size of the partitions of all iterations will be equal. Average condition occurs when we apply quick sort on a random array.

The diagram below shows an experimental result how quick sort performs in various conditions.

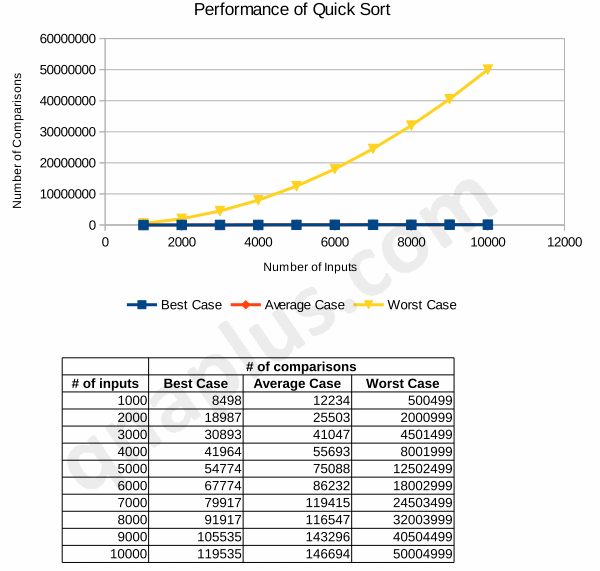
We can see that the actual number of comparisons in worst case is much higher than the best or average case. Another thing to notice here is that the growth rate of number of comparisons with respect to the number of inputs is also much much higher in worst case than best or average case.

If you also want to contribute, click here.