Bubble Sort is one of the most fundamental sorting algorithms, often introduced early in programming courses due to its simplicity. Although not efficient for large datasets, it serves as a great starting point for understanding sorting mechanisms. In this post, we’ll learn how Bubble Sort works, explore its variations, and implement it in C with optimized examples.
What is Bubble Sort?
Bubble Sort repeatedly compares adjacent elements in an array and swaps them if they are in the wrong order. This process continues until the array is sorted. While simple, Bubble Sort is less efficient compared to advanced sorting algorithms like Quick Sort or Merge Sort.
Key Characteristics:
- Time Complexity:
- Best Case (Θ(n)): Occurs when the array is already sorted. The algorithm completes in a single pass without any swaps.
- Worst Case (Θ(n²)): Occurs when the array is sorted in reverse order. The algorithm performs the maximum number of comparisons and swaps.
- Average Case (Θ(n²)): On average, the algorithm performs half the comparisons and swaps of the worst case.
- Space Complexity:
- In-Place Sorting (O(1)): Bubble Sort requires no additional memory, as the sorting happens within the input array.
- Stability:
- Bubble Sort maintains the relative order of equal elements, making it a stable sorting algorithm.
Bubble Sort Algorithm
- Compare adjacent elements.
- Swap them if they are out of order.
- Repeat for each element until no swaps are needed.
- After each pass, the largest unsorted element is placed at the correct position.
Graphical Illustration
Below is a visualization of how Bubble Sort organizes the elements step-by-step:
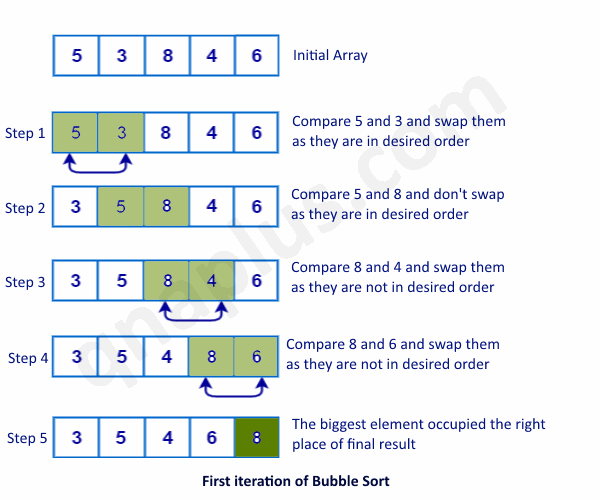
Notice how each outer loop iteration places the next largest element in its correct position.
Implementation of Bubble Sort in C
We’ll explore two variations of Bubble Sort—a basic version and an optimized version.
Variation 1:
This straightforward approach uses two nested loops for sorting.
test.c#include <stdio.h> void bubble_sort(int *arr, int n) { int i = 0, j = 0; int tmp = 0; for(i = 0; i < n-1; i++) { for (j = 0; j < n-1; j++) { if(arr[j+1] < arr[j]) { tmp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = tmp; } } } } #define MAX_SIZE 64 int main() { int arr[MAX_SIZE]; int n, i; printf("Enter the size of the array: "); scanf("%d", &n); printf("Enter the array elements:\n"); for(i = 0; i < n; i++) { printf("arr[%d]: ", i); scanf("%d", arr + i); } printf("The entered array:\n"); for(i = 0; i < n; i++) { printf("%d ", arr[i]); } printf("\n"); bubble_sort(arr, n); printf("The sorted array:\n"); for(i = 0; i < n; i++) { printf("%d ", arr[i]); } printf("\n"); return 0; }
The main() function first takes an array as input and calls the bubble_sort() function to sort that array.
Output
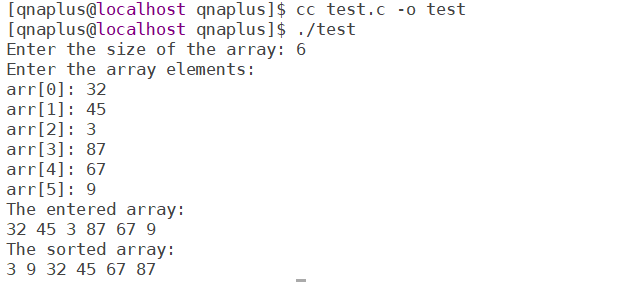
This version of the bubble_sort() function is very easy to understand. Here both the outer loop and inner loop iterate n-1 times. The inner loop starts from the first element and checks with the next element whether they are in right order. If not, then swaps them.
For example, if the current element (indexed by j) is greater than the next element (indexed by j+1), then we swap them. Then control moves to the next element.
In this case, we’ll always have (n-1)*(n-1) comparisons which is more than the maximum comparisons required by bubble sort even in the worst case scenario.
Variation 2:
Let’s see how we can improve the algorithm little bit and minimize the number of comparisons.
After completion of every iteration of the outer loop, one element is placed in the right location. That means the inner loop does not need to iterate (n-1) times all the time. It can iterate one less time after every outer loop iteration.
void bubble_sort(int *arr, int n)
{
int i = 0, j = 0;
int tmp = 0;
for(i = 0; i < n-1; i++)
{
for (j = 0; j < n-i-1; j++)
{
if(arr[j+1] < arr[j])
{
tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
}
}
}
}We changed the loop from:
for (j = 0; j < n-1; j++)to
for (j = 0; j < n-i-1; j++)As the value of i increases, the inner loop iterates less. That way we can reduce the total number of comparisons.
Variation 3:
We can further improve the logic by terminating the outer loop if no swapping is performed by the inner loop.
No swapping in inner loop means the array already became sorted. No need to continue the outer loop after that.
void bubble_sort(int *arr, int n)
{
int i = 0;
int tmp = 0;
int swapped = 0;
do
{
swapped = 0;
for (i = 0; i < n-1; i++)
{
if(arr[i+1] < arr[i])
{
tmp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = tmp;
swapped = 1;
}
}
n = n - 1;
} while (swapped == 1);
}Here we changed the outer loop from ‘for‘ to ‘do-while’ . We could continue with the for loop also, but in this situation, a do-while loop is more appropriate.
We are reducing n by 1 (n = n-1) at the end of the inner loop such that it iterates one less time in next iteration.
The inner loop sets flag (swapped) if it performs a swapping. And outer loop continues only if ‘swapped’ flag is set.
Variation 4:
We can improve further!
In previous implementations, we were reducing the inner loop iteration by one for every outer loop iteration. But we can remember where (at which index) the last swapping happened in the inner loop. The rest of the array after that is already sorted.
In the next outer loop iteration, we can stop the inner loop where it did the last swapping in previous iteration.
void bubble_sort(int *arr, int n)
{
int i = 0;
int tmp = 0;
int newn = 0;
int swapped = 0;
do
{
swapped = 0;
for (i = 0; i < n-1; i++)
{
if(arr[i+1] < arr[i])
{
tmp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = tmp;
swapped = 1;
newn = i + 1;
}
}
n = newn;
} while (swapped == 1);
}Here the newn variable remembers where the inner loop did last swapping. Next time, the inner loop will go up to that point (up to the newn).
This is the most optimized implementation of bubble sort.
Performance of Bubble Sort
In this section, we’ll see how bubble sort performs in various conditions.
Worst Case:
The worst case is when the array is in the opposite order before we start sorting. For example, if we want to sort an array in ascending order, the array is in descending order at the beginning.
In the worst case scenario, the running time of bubble sort in Big-O notation is O(N2).
The diagram show how our four variations perform in the worst case.
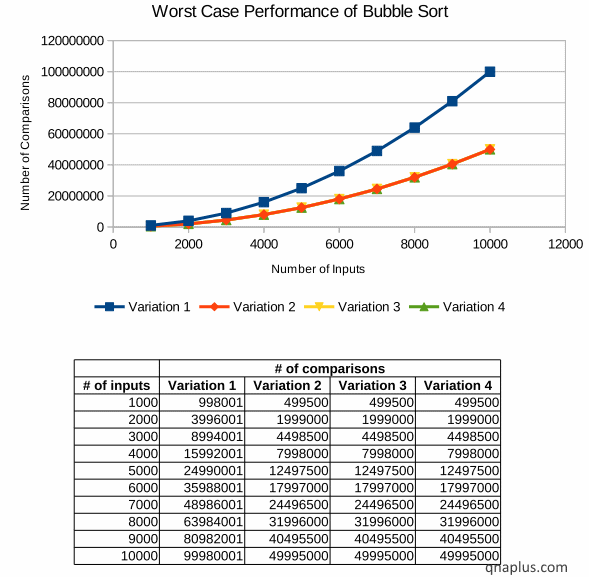
Here we can see how the number of comparison increases with the increase of the number of input elements. And the number of comparisons is directly proportional to the running time.
From the graph we can see that the first variation takes maximum number of comparisons. Other three variations take equal number of comparisons but less than that of the first variation.
We should also notice one important thing that the growth rate of all four variations is the same. If we double the number of inputs then the number of comparison becomes four times. If we increase the number of elements by four times then the number of comparisons increases by sixteen times.
It means the growth rate is O(N2).
Average Case:
The average case is when the array is in random order at the beginning.
In the average case also, the running time is O(N2).
The diagram below shows the four variations performance in this scenario.
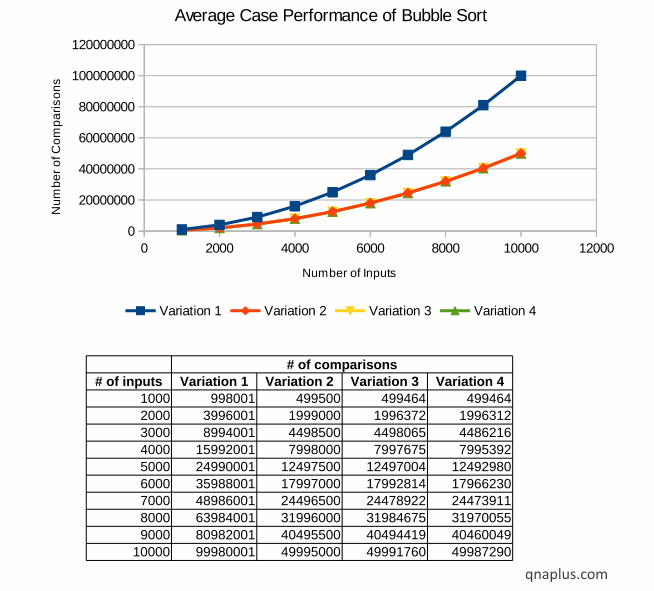
We can see that the first variation takes maximum number of comparison, then the second one, then the third one. The fourth variation takes least number of comparisons. But here also the comparison growth rate is the same, i.e. O(N2). If we double the number of inputs, the number of comparison will become four times.
Best Case:
The best case scenario is when the array is already sorted.
In this scenario, the bubble sort running time is O(N).
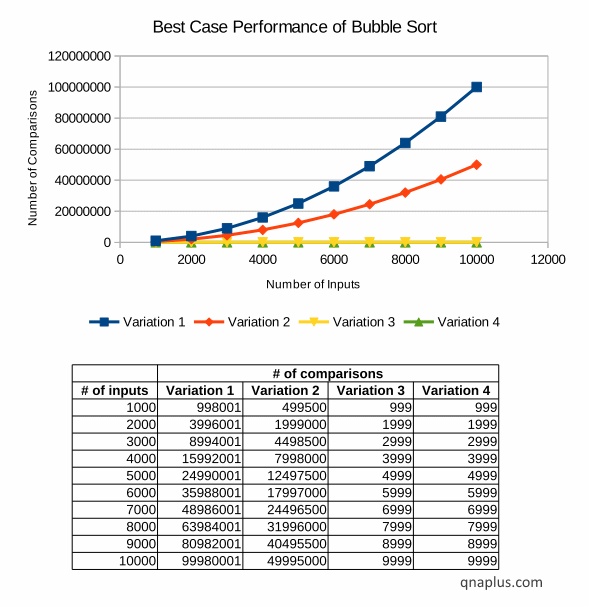
Here the comparison growth rate of first two variations is still O(N2). Second variation is slightly better than the first one in terms of actual number of comparisons. But our last two variations perform much better than the first two. The growth rate of third and fourth variations is linear. They always take n-1 comparisons.
We can see that choice of implement is important in terms of performance. The forth variation performs the best in all conditions – at least not worse than any other.