Binary search is an efficient searching technique that is used to search a key in a sorted array. In every iteration, searching scope is reduced to half. That’s why it is called Binary Search or Half Interval search.
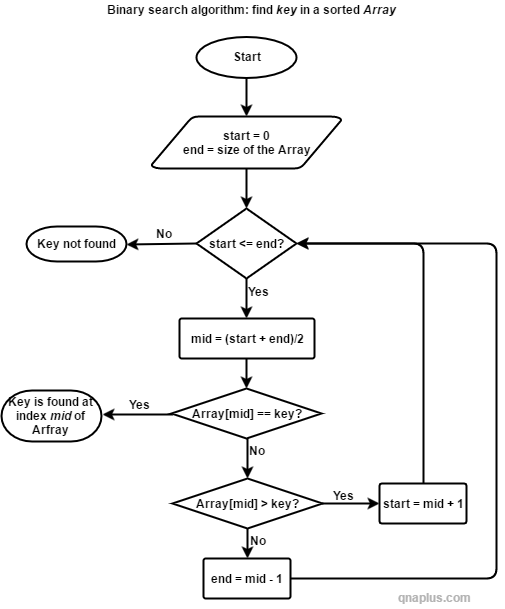
Binary Search Algorithm
- If the middle element of the sub-array is equal to the key, then the search is complete. Sub-array is specified by start and end indexes. So the middle element is (start+end)/2 -th element.
- If the key is smaller than the middle element, then the new end will be (mid – 1). Else the new start will be (mid+1). Here mid is the index of the middle element.
- Repeat steps 1 and 2 until the key is found or end becomes less than start.
Here we assumed that the array was sorted in ascending order. Algorithm would be very similar in case of descending ordered array.
Graphical Illustration
We’ll try to understand the bubble sort algorithm graphically. In this example, we have 11 elements in the array and we’ll search for the key 23.

In the first iteration, our search scope is the whole array of eleven elements. So we will compare the key 23 with the middle element of the array. Here the middle element is 9 which is not equal to 23. So we’ll move to the next iteration.
As our key (23) is greater than the middle element (9), there is no chance that the key (23) will be present in the first half. So, we’ll totally forget the first half and the middle element. For the next iteration, our searching scope is the second half of the array.

Middle element of the second half is equal to the key. So the searching ends here and the key is found at 9-th index.
Binary Search Flowchart
Binary Search Program
#include <stdio.h>
int binary_search(int *arr, int size, int key)
{
int start = 0;
int end = size - 1;
int mid = 0;
while(start <= end)
{
mid = (start + end) / 2;
if (key == arr[mid]) return mid;
if (key < arr[mid])
end = mid - 1;
else
start = mid + 1;
}
return -1;
}
int main()
{
int arr[] = {3, 5, 9, 12, 23, 45, 56, 58, 63, 65, 78, 89, 90};
int key = 0, array_size, result, i;
array_size = sizeof(arr) / sizeof(int);
printf("The array: ");
for(i = 0; i < array_size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
printf("Enter a key to search: ");
scanf("%d", &key);
result = binary_search(arr, array_size, key);
if(result == -1) {
printf("Key %d is not present in the array.\n", key);
} else {
printf("Key %d is present in the array at %d-th position.\n", key, result);
}
return 0;
}
This program has a sorted array and it takes the key as input. The binary_search() function implement the algorithm. It takes the array, array size and the key as input.
If the key is present in the array the function returns the position (index) of the array. If the key is not found, then it returns -1.
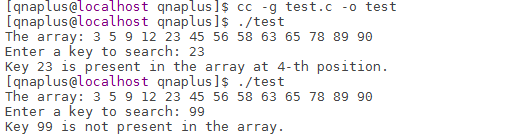
Here is the output.
Recursive Version of Binary Search Function
We can make the binary_search() function a recursive one.
#include <stdio.h>
int binary_search(int * arr, int start, int end, int key)
{ int mid = 0;
if (start > end) return -1;
mid = (start + end) / 2;
if (key < arr[mid])
return binary_search(arr, start, mid - 1, key);
if (key > arr[mid])
return binary_search(arr, mid + 1, end, key);
return mid;
}
int main()
{
int arr[] = {3, 5, 9, 12, 23, 45, 56, 58, 63, 65, 78, 89, 90};
int key = 0, array_size, result, i;
array_size = sizeof(arr) / sizeof(int);
for(i = 0; i < array_size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
printf("Enter a key to search: ");
scanf("%d", &key);
result = binary_search(arr, 0, array_size - 1, key);
if(result == -1) {
printf("Key %d is not present in the array.\n", key);
} else {
printf("Key %d is present in the array at %d-th position.\n", key, result);
}
return 0;
}This version of the function takes the array, start index, end index and the key as input. We set start as 0 and end as (array size -1) from the main().
When We can Apply Binary Search
We can’t apply binary search everywhere – certain criteria need to be met.
- Array must be sorted. This is the most important criteria. We can not apply binary search on an unsorted array.
- Every element needs be accessed directly. This is true for C array. We can access any element of an array directly using an index like arr[i], where arr is the array name and i is the index of the element. But we can not apply binary search algorithm on a linked list even if the linked list is sorted.
Performance
Binary search is more efficient in most cases compare to linear search.
Best Case Scenario
Best case scenario occurs when the key is present at the middle of the array. Key will be found at the very first attempt. That means it is a constant time operation. So the running time in Big-O notation is O(1).
Worst Case Scenario
Worst case scenario occurs when the key is present at the edge of the array. Either the first or the last element is the key. In that case the algorithm will take at most log2N comparisons to find the key. For example, if the array has 1024 elements, then 10 comparisons are required. If you double the array size the number of comparisons will increase by 1 only. In Big-O notation the running time is O(logN).
Average Case Scenario
Average case means the key is at any random position. So the number of comparison varies from 1 to log2N. If we double the array size, the number of comparisons will increase at most by 1. In this case the running time is still O(logN) in Big-O notation.