In computer and data communication, endianness refers to the ordering of bytes of a multi-byte data type in memory. In little endian systems, least significant byte is stored first in the memory and subsequent bytes are stored in the higher memory addresses. Similarly, in big endian systems, bytes are stored in the reverse order, i.e. most significant byte is stored first and the subsequent bytes are stored in the higher memory addresses. In other words, less the significance of the byte, higher the memory address it will be stored in. All that is fine. But what is significance of a byte? How they are differently stored in big endian and little endian systems?
What is significance of a byte?
All these definitions talk about the significance of bytes but what the hell it is. Well, before talking about the byte and memory address, I will start will a familiar daily life example.
We represent counts or numbers in digit like 1, 2, 3, 4, … etc. As you can imagine, one digit is not enough to represent all numbers. If we want to count twelve thousand three hundred forty five, we represent that as 12345. Here we used five digits. Whenever we represent a number in multiple digits, the question of significance of the digits comes into the picture. Are the significance or importance of all digits same or different? To want understand that, first we have to define significance.
Let me define significance in this way:
– We will do similar changes to two digits of a number.
– We will see the effect of change of each digit.
– If the effect of change of the first digit is higher than the effect of change of the second digit, the significance of the first digit is higher than the second.
Lets come back to our example number 12345. It has five digits in five positions. We will start the positions from left to right.
– Digit in first position is 5, digit in second position is 4 and so on.
– Increase the digit of the first position by 1. So the number becomes 12346. So the overall impact is (12346 – 12345) 1.
– Now we’ll do the same thing to the digit of fifth position, increase it by 1. So the number becomes 22345. Here the overall impact is (22345 – 12345) 10000.
– So the impact of the same change on the fifth digit is much higher than the first digit. So as per our definition, significance of the fifth digit is higher than the first.
– So in our example significance of any left side digit is higher than that of any left side digit.
Similar analogy applies for bytes of a multi-byte data type. Data is stored in the computer memory in a series of bytes. As a byte has 8 bits, one byte can represent a number from 0x00 (0) to 0xFF (255) if we take integer as an example. If we want to store an integer bigger than 0xFF (255), then multiple bytes are required. For example if we want to store a number 0x11223344 (287454020), we’ll need 4 bytes. Binary representation of the number will be

- If we change the 7th bit of the byte 00010001 (0x11) from 0 to 1, the number will become 10010001 00100010 00110011 01000100 or 0x91223344.
- Here the overall impact is (0x91223344 – 0x11223344) 0x80000000 or 2147483648 in decimal.
- Similarly if we change the 7th bit of the byte 01000100 (0x44), the number will become 00010001 00100010 00110011 11000100 or 0x112233C4.
- So the overall impact is 0x112233C4 – 0x11223344 = 0x80 or 128 in decimal.
As impact of similar change of byte 00010001 (0x11) is higher than the byte 01000100 (0x44), so the significance of byte 00010001 (0x11) is higher that byte 01000100 (0x44).
Big Endian vs Little Endian
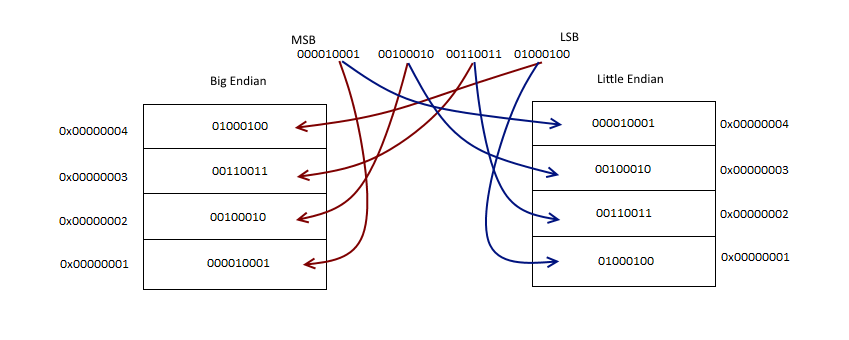
So far we understood the significance of a byte. As I mentioned earlier, data is stored in computer memory in form of byte series. All bytes are addressed by some number. Two consecutive bytes will be addressed by consecutive numbers. Let say the integer of our example 0x11223344 (00010001 00100010 00110011 01000100) will be stored in four consecutive bytes starting from 0x00000001 to 0x00000004. We already know that the significance of byte 00010001 is highest, then byte 00100010 and so on. 01000100 is the least significant byte.
As in big endian system most significant byte will be stored first, 00010001 will be stored at 0x00000001, 00100010 at 0x00000002, 00110011 at 0x00000003 and 01000100 at 0x00000004.
And in little endian system least significant byte will be stored first, so 01000100 will be stored at 0x00000001, 00110011 at 0x00000002, 00100010 at 0x00000003 and 00010001 at 0x00000004.